Як швидко та точно розрахувати складні відсотки
Дізнайтеся, як розрахувати складні відсотки за допомогою чітких формул, реальних прикладів та практичних порад, щоб збільшити свої заощадження вже сьогодні.

Рекомендовані розширення
Розуміння формули складних відсотків
Шукаєте зрозумілий спосіб побачити, як ваші заощадження можуть зростати? Формула складних відсотків, A = P(1 + r/n)^(nt), об'єднує ваш початковий внесок, процентну ставку, частоту нарахування відсотків і час в одну потужну формулу.
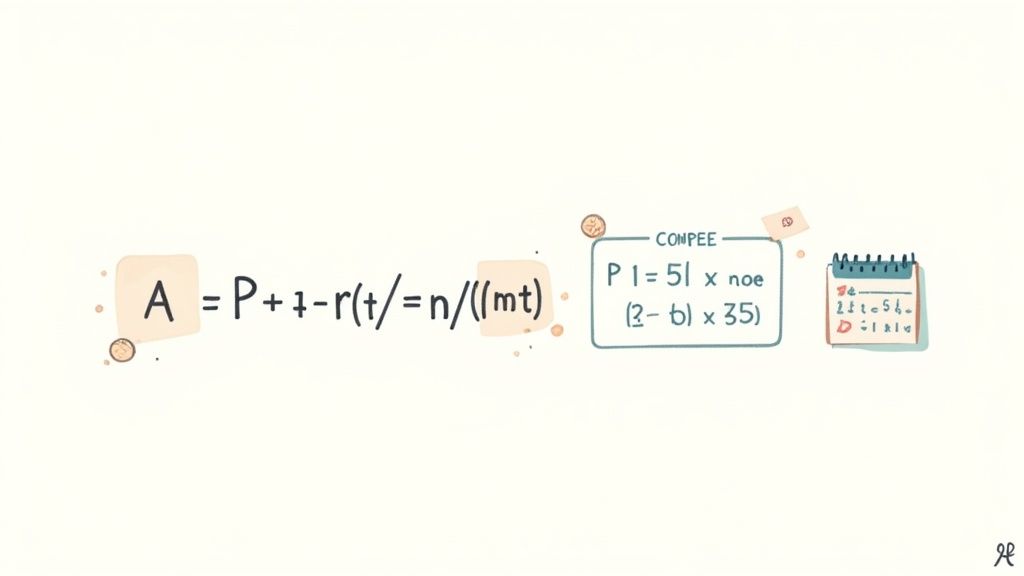
Складні відсотки означають, що ви отримуєте відсотки на відсотки — і цей ефект дійсно проявляється протягом кількох періодів. Щоб зрозуміти це, давайте розглянемо кожен компонент:
- P (Основна сума): Ваш початковий баланс
- r (Ставка): Річна процентна ставка, виражена у десятковому вигляді
- n (Частота): Скільки разів відсотки нараховуються кожного року
- t (Час): Тривалість вашої інвестиції в роках
- A (Сума): Сума, яку ви отримуєте після нарахування відсотків
Ви часто бачите, як банки рекламують річну ставку, але застосовують її щомісяця або щодня. Розуміння різниці між річною процентною ставкою та фактичним графіком нарахування допоможе уникнути неприємних сюрпризів.
Уявіть, що ви відкриваєте рахунок з високими відсотками на $10,000 під 5% річних, нарахованих щомісяця протягом 5 років. Ось як зводяться разом цифри:
- Переведіть ставку в десяткову форму: r = 0.05
- Знайдіть періодичну ставку: r ÷ n = 0.05 ÷ 12
- Додайте одиницю до результату: 1 + 0.004167 = 1.004167
- Застосуйте показник до всіх періодів: (1.004167)^60
- Помножте на основну суму: 10,000 × 1.2834 ≈ $12,834
Цей приріст становить трохи більше 28% прибутку, і все це без додавання ще одного цента.
Підсумок змінних складних відсотків
Нижче наведено швидкий довідник для кожного символу у нашій формулі, доповнений прикладом значень, взятих з наведеного вище прикладу. Тримайте цю таблицю під рукою, коли експериментуєте з різними ставками, частотами або часовими горизонтами.
| Змінна | Визначення | Приклад Значення |
|---|---|---|
| P | Основна сума | $10,000 |
| r | Річна процентна ставка (десяткове число) | 0.05 |
| n | Періоди нарахування на рік | 12 |
| t | Час в роках | 5 |
| A | Майбутня вартість після нарахування | $12,834 |
Тримайте ці визначення в пам'яті, коли досліджуєте сценарії щомісячного, щоденного або навіть безперервного нарахування. З таблицею поруч, налаштування будь-якої змінної в електронній таблиці або калькуляторі стає простим.
Розуміння ключових змінних

Розуміння складних відсотків починається з п'яти основних елементів: основна сума (P), річна ставка (r), частота нарахування (n), часовий горизонт (t) та результуюча сума (A). Зміна будь-якого з цих елементів може суттєво вплинути на ваш кінцевий баланс.
Уявіть, що ви вносите $5,000 під 5% річних. Тепер підвищте ставку до 6% або змініть нарахування з річного на щомісячне. Ви побачите, як навіть незначні зміни можуть змінити довгострокове зростання.
- Основна сума (P): Ваш початковий внесок або інвестиція.
- Річна ставка (r): Темп зростання, виражений у десятковому вигляді (0.05 дорівнює 5%).
- Частота (n): Як часто відсотки нараховуються кожного року (1, 12, 365).
- Час (t): Тривалість інвестиції в роках.
- Сума (A): Майбутня вартість після нарахування.
Дослідження основної суми та ставки
Розуміння того, як P та r взаємодіють, допомагає встановити реалістичні цілі. Внесіть $1,000 під 4% на 10 років, і ви використовуєте A = P × (1 + r)^t, що стає 1,000 × (1.04)^10. Це обчислення дає приблизно $1,480.
Вибір розумної ставки означає дослідження історичних доходів та поточних ставок заощаджень. Наприклад, очікувати двозначних прибутків, коли найкращі ощадні рахунки коливаються навколо 1.5%, — це мрії.
“Невеликі відсоткові різниці протягом десятиліть можуть подвоїти або потроїти ваш закінчений баланс.”
— Інсайт фінансового планування
Далі давайте подивимося, як частота нарахування посилює ці ефекти.
Коригування частоти та часу
Перехід від річного до щомісячного нарахування додає додаткові періоди. При 5%, A = P × (1 + 0.05/12)^(12 × 10) перетворює той же 10-річний період на приблизно $1,647 замість $1,628.
Тримайте ці поради в пам'яті:
- Переведіть відсотки в десяткові числа перед будь-яким діленням.
- Зіставте ваші n та t одиниці (місяці проти років).
- Зберігайте округлення для остаточного результату, щоб уникнути зсуву.
Якщо ви розширите ставку 3% на 20 років з щоденним нарахуванням, ефективна прибутковість зростає більш ніж на 2% у порівнянні лише з річним нарахуванням. Це чітке нагадування про те, що частота - це не просто деталь, а рушійна сила.
Для більш глибокого занурення ознайомтеся з посібником ShiftShift щодо розрахунку складних відсотків. Практикуйте введення різних значень, і ви розвинете інтуїцію для планування розумніших інвестицій.
Розрахунок складних відсотків вручну
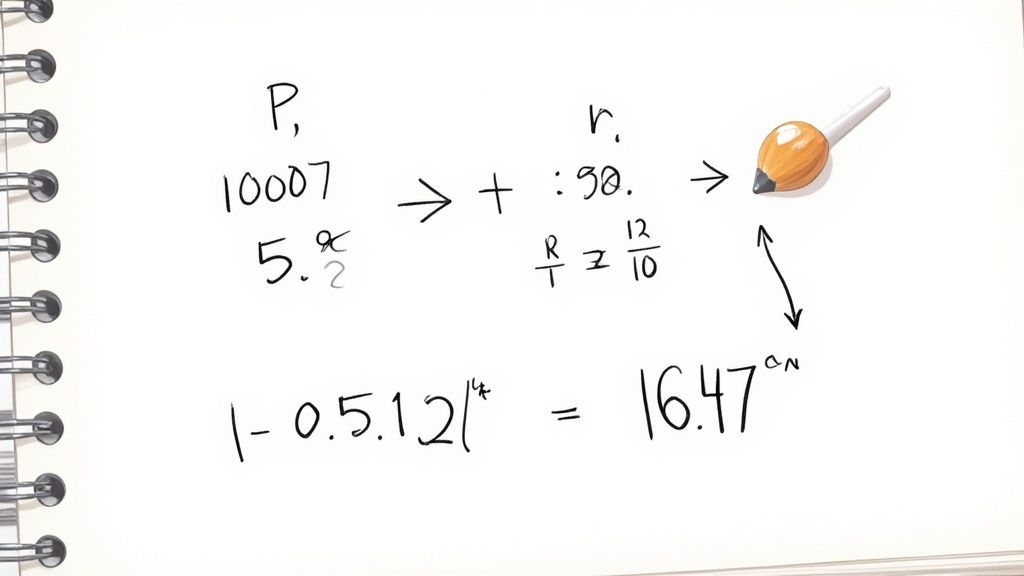
Коли ви працюєте з формулою вручну, механіка зростання дійсно починає мати сенс. Нижче ми розглянемо, як відсотки накопичуються при річному, місячному, щоденному та безперервному нарахуванні.
Приклад річного нарахування
Простий річний модель використовує A = P(1 + r)ᵗ. Спочатку перетворіть процентну ставку в десятковий формат.
- Перетворіть 5% на 0.05.
- Розрахуйте (1 + 0.05)¹⁰ = 1.6289.
- Помножте на основну суму $10,000, щоб отримати $16,289.
Уявіть, що ви вносите $10,000 під 5% на десять років—ваш баланс зростає до $16,289, показуючи, як річне повторне інвестування сприяє стабільному зростанню.
Місячний розрахунок
Перехід до місячного нарахування змінює формулу на A = P(1 + r/12)^(12t). Вам просто потрібно розділити ставку та відкоригувати показник.
- Розділіть 0.05 на 12, щоб отримати 0.004167.
- Додайте 1, потім підніміть результат до 120-го ступеня за десятиліття.
- Помножте на $10,000, щоб отримати приблизно $16,470.
Цей додатковий цикл нарахування кожного місяця трохи підвищує вашу прибутковість у порівнянні з річним підходом.
Для ширшого контексту, MSCI World Index в євро забезпечив 10.49% CAGR з 1978 по 2025 рік, перетворивши €1,000 приблизно на €85,000. Дивіться повні дані в даних NYU Stern.
Щоденне та безперервне нарахування
Коли відсотки нараховуються щодня, використовуйте A = P(1 + r/365)^(365t). Цей щоденний ритм підвищує прибутковість.
- Розділіть річну ставку на 365, потім підніміть результат до 365t.
- Для справжнього безперервного нарахування змініть на A = P × e^(r t) і дайте природному показнику зробити свою магію.
При 5% протягом десяти років безперервне зростання дає A = P × e^(0.5), приблизно $16,487—теоретичний максимум у порівнянні з дискретними методами.
Сценарій довгострокового зростання
Розширте горизонт, і сила нарахування дійсно сяє. Інвестуйте $10,000 під 10.49% на 30 років, і A = P(1 + r)ᵗ зросте приблизно до $217,000.
Показники, такі як MSCI, нагадують нам, що навіть невеликі різниці в ставках стають величезними сумами, коли ви даєте їм десятиліття для роботи.
Невеликі зміни в ставці або частоті можуть перетворитися на тисячі доларів, коли терпіння на вашому боці.
Поради для ручних розрахунків
- Тримайте свої десяткові дроби точними до останнього кроку, щоб уникнути зсуву округлення.
- Відповідайте своїм одиницям часу з частотою нарахування, яку ви обираєте.
- Перевіряйте кожен запис за допомогою простого калькулятора або електронної таблиці—прості помилки часто є звичними винуватцями.
Практика цих ручних кроків розвиває вашу інтуїцію. Далі ми побачимо, як електронна таблиця може автоматизувати все це.
| Частота | Формула | Приклад результату |
|---|---|---|
| Річна | A = P(1 + r)ᵗ | $16,289 |
| Місячна | A = P(1 + r/12)^(12t) | $16,470 |
| Щоденна | A = P(1 + r/365)^(365t) | $16,487 |
| Безперервна | A = P × e^(r t) | $16,487 |
Ця таблиця підкреслює, як частіше нарахування м'яко підвищує ваш остаточний баланс. Далі: освоєння цих розрахунків в електронній таблиці.
Автоматизація складних відсотків за допомогою електронних таблиць та онлайн-інструментів
Створення власного калькулятора складних відсотків в електронній таблиці є величезним заощадженням часу при тестуванні різних сценаріїв. Як тільки ви зв'яжете P, r, n та t з клітинками, вбудовані функції виконують основну роботу.
В Excel або Google Sheets ви налаштовуєте клітинки введення для основної суми, ставки, частоти та тривалості.
Програмне забезпечення потім обробляє математичні розрахунки.
- Використовуйте функцію POWER для (1 + rate / n)^(n×t), щоб точно відстежувати зростання.
- Застосуйте EDATE або формули заповнення для автоматичного створення щомісячного або щоденного графіка.
- Додайте випадаючі списки валідації даних, щоб користувачі могли вибирати процентні ставки та частоту нарахування без помилок.
Форматування вхідних клітин
Чітко позначте кожну клітину — подумайте про "Основна сума", "Річна ставка", "Нарахування на рік" та "Роки". Таким чином, будь-хто, хто відкриває таблицю, точно знає, де вводити значення.
Заблокуйте свої клітини з формулами та змішуйте відносні з абсолютними посиланнями. Це запобігає випадковим перезаписам, поки ви змінюєте вхідні дані.
Побудова графіків зростання
Швидка лінійна або площинна діаграма може виявити зразки зростання, які ви можете пропустити в сирих числах. Виберіть ваші стовпці часових рядів та майбутньої вартості, а потім вставте діаграму, яку ви віддаєте перевагу.
- Форматуйте мітки серій з їх ставкою, щоб ви могли порівнювати сценарії поруч.
- Додайте назви осей, щоб відрізнити основні суми від часових інтервалів.
- Використовуйте маркери на ключових датах, щоб підкреслити стрибки нарахування.
Користувацькі кольори та символи оживляють ці точки перегину, що робить легшим виявлення впливу різних ставок.
Цей вид показує, як формули автоматично оновлюють підсумки та оновлюють діаграму в момент, коли ви змінюєте змінну. Ознайомтеся з нашим калькулятором складних відсотків у браузері для миттєвого тестування сценаріїв у вашому браузері.
Захист від помилок
Один єдиний друкарський помилок у посиланні на клітину може спотворити вашу всю модель. На щастя, вбудоване перевірка помилок та умовне форматування позначать будь-які дані, що виходять за межі.
- Переконайтеся, що введені ставки є десятковими (наприклад, 0.05, а не 5%), щоб зберегти одиниці послідовними.
- Перевірте, що випадаючий список частоти відповідає одиниці часу у вашому експоненті.
- Заблокуйте заголовки рядків, щоб мітки залишалися на місці, коли ви прокручуєте довгі набори даних.
Використання бібліотек шаблонів
Попередньо створені шаблони прискорюють налаштування та мінімізують помилки у формулах. Онлайн-репозиторії та галерея шаблонів Sheets є чудовими стартовими точками.
- Встановіть спільні доповнення з фінансовими шаблонами.
- Налаштуйте клітини основної суми та ставки шаблону відповідно до ваших припущень.
- Поділіться готовою таблицею з колегами для послідовного моделювання.
Шаблони виконують роль навчальних інструментів і швидких шляхів, коли вам потрібно розрахувати складні відсотки в кількох сценаріях.
Автоматизація цих розрахунків дозволяє вам швидше ітераційно працювати та налаштовувати ваші фінансові прогнози. Чи будуєте ви з нуля, чи адаптуєте шаблон, ви швидко оволодієте складними відсотками.
Порівняння частот нарахування та реального впливу
Навіть коли річна ставка залишається на рівні 5%, фінальна сума помітно змінюється залежно від того, як часто нараховуються відсотки. Протягом десятиліття $10,000 може зрости до $16,289 при річному нарахуванні. Якщо перейти на щомісячне, ви побачите близько $16,470. Якщо перейти на безперервне нарахування, ця сума досягне $16,487.
Банки часто наводять піврічні або квартальні графіки. У цьому ж прикладі, нарахування двічі на рік призводить до $16,330, тоді як чотири рази на рік підвищує його до $16,365. Щоденне нарахування трохи нижче щомісячного — приблизно $16,487 — показуючи, як частіші додавання поступово підвищують вашу загальну суму.
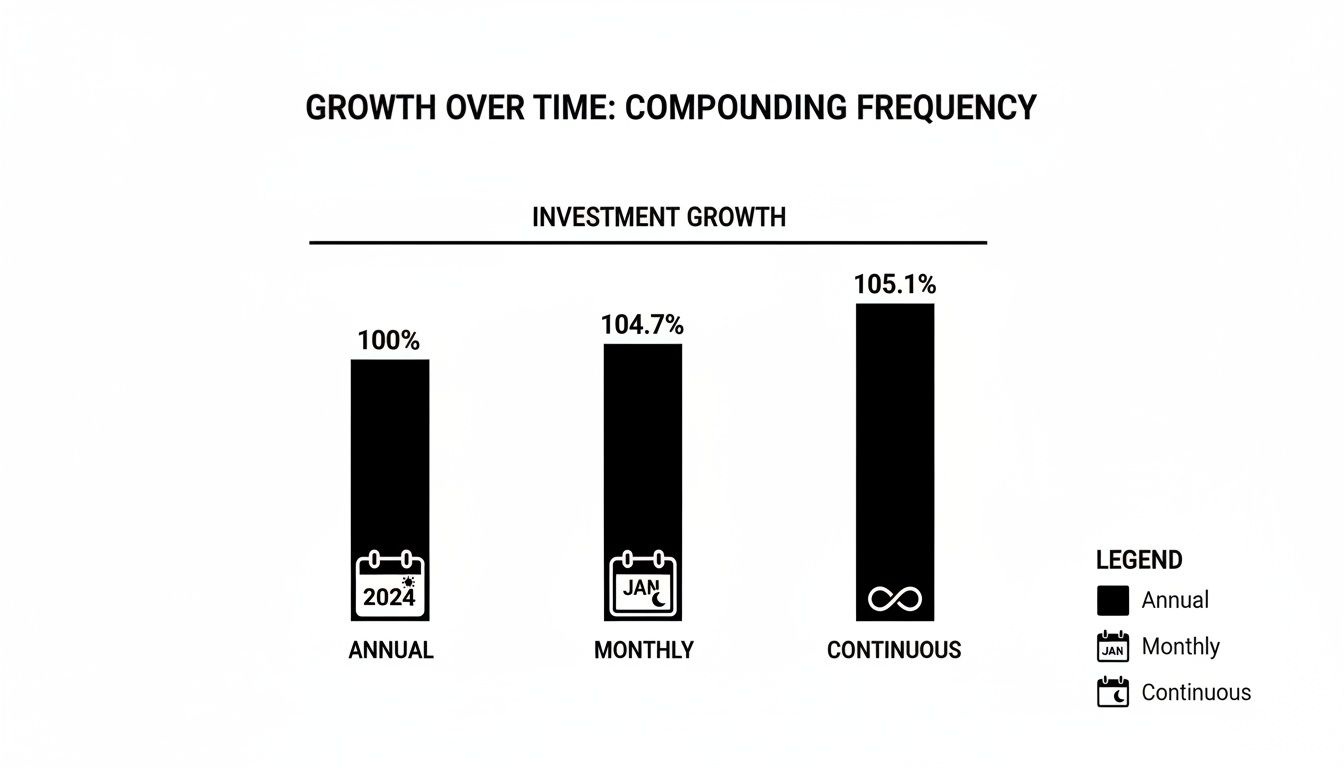
Вплив частоти нарахування
Нижче наведено швидке порівняння формул і кінцевих залишків через десять років при 5%:
Швидко погляньте, як ці інтервали співвідносяться:
| Частота | Формула | Результат |
|---|---|---|
| Щорічно | A = P (1 + r)ᵗ | $16,289 |
| Піврічно | A = P (1 + r/2)^(2t) | $16,330 |
| Квартально | A = P (1 + r/4)^(4t) | $16,365 |
| Щомісячно | A = P (1 + r/12)^(12t) | $16,470 |
| Щоденно | A = P (1 + r/365)^(365t) | $16,487 |
| Безперервно | A = P × e^(rt) | $16,488 |
Навіть якщо безперервне нарахування представляє теоретичний максимум, ви можете обробляти щоденні або безперервні моделі з більшістю фінансових калькуляторів та функцій електронних таблиць.
Історична перспектива на складні доходи
Щоб оцінити довгострокову силу нарахування, розгляньте це: одна £1, інвестована в американський фондовий ринок у 1900 році, зросла б до приблизно £3,703 на сьогоднішній день при 6.9% реальному річному доході. Така ж сума на ринку Великобританії, при 4.8%, становила б лише £341. Реальний дохід Австралії 6.4%, тим часом, перетворює цей фунт приблизно на £2,134 за 124 роки.
Для отримання додаткової інформації про ці показники, ознайомтеся з цими даними про глобальні ринкові доходи.
“Складні відсотки перетворюють скромні заощадження на багатства, коли ви дозволяєте часу виконати свою роботу.”
Основні висновки з цих графіків та реальних прикладів:
- Вища частота нарахування відсотків забезпечує трохи кращі ефективні ставки
- Невелика різниця в річних доходах значно множиться протягом десятиліть
- Електронні таблиці або калькулятори в браузері без зусиль моделюють щоденне та безперервне нарахування відсотків
- Завжди враховуйте будь-які додаткові збори або мінімальні залишки у порівнянні з граничними вигодами
- Вибір щомісячного нарахування часто є оптимальним для повсякденних заощаджень; обирайте безперервне для розширених прогнозів
В кінці кінців, нарахування завжди працює на основну суму плюс нараховані відсотки. Переконайтеся, що ваші інструменти правильно відстежують кожен період, щоб ви могли планувати з упевненістю.
Поширені помилки, яких слід уникати при прогнозуванні зростання
Прогнозування зростання з використанням складних відсотків є оманливо простим — і дуже легко допустити помилку. Переплутайте номінальну ставку з реальною ставкою, і ваші прогнози можуть значно відхилитися від реальності. Пам'ятайте, що номінальні показники не враховують інфляцію, тоді як реальні ставки коригуються відповідно до справжньої купівельної спроможності ваших грошей.
- Несумісні одиниці зривають розрахунки. Завжди узгоджуйте часові періоди — роки, місяці або дні — перед тим, як вводити числа.
- Неконвертовані відсотки перетворюють 0.05 на 5, якщо ви забудете про десяткову крапку, що спотворює результати.
- Ігноровані грошові потоки приховують регулярні зняття або додаткові внески, спотворюючи ваш остаточний баланс.
Перевірка вхідних даних
Швидка перевірка ваших даних може зберегти безліч головного болю. Сучасні електронні таблиці пропонують вбудовану перевірку даних та перевірку помилок — використовуйте їх.
Швидкий погляд на несумісні одиниці одного разу врятував мене від 20% завищення.
Варто перевірити, щоб кожна ставка була в десятковій формі (наприклад, 5% як 0.05) і щоб ваша частота нарахування відповідала обраному періоду.
Критичне тлумачення результатів
Числа не брешуть — але вони можуть ввести вас в оману, якщо ви сприймаєте їх за чисту правду. Завжди запускайте простий бенчмарк поряд з вашою детальною моделлю.
- Порівняйте ваш час подвоєння з Правилом 72, щоб виявити серйозні аномалії.
- Перевірте, чи дійсно додаткові внески підвищують баланс.
- Переконайтеся, що періодичні зняття зменшують остаточну суму.
- Слідкуйте за округленням: зміни більше ніж 0.1% можуть свідчити про глибшу проблему з формулою.
Я бачив, як зайве нульове число завищує прогноз на 10×. Не дозволяйте маленькій помилці зруйнувати весь ваш аналіз.
Швидкі стратегії перевірки
Перед завершенням проведіть швидкий, але зосереджений аудит вашої електронної таблиці:
- Перегляньте формули на наявність відсутніх дужок або неправильних посилань на клітинки
- Підтвердіть, що n (періоди нарахування) та t (час) використовують однакові одиниці
- Застосуйте кольорові акценти для групування вхідних даних, розрахунків та виходів
Другий погляд часто виявляє те, що години роботи пропустили.
Запросіть колегу переглянути вашу роботу або поділіться вашою таблицею через ShiftShift Extensions для нових перспектив. Регулярно оновлюйте свої шаблони та правила перевірки, щоб майбутні прогнози були бездоганними.
Практичні поради
- Подвійно перевірте припущення щодо інфляції на основі останніх даних CPI.
- Автоматизуйте повторювані перевірки за допомогою Калькулятора складних відсотків від ShiftShift Extensions, щоб зменшити кількість ручних помилок.
- Зберігайте чітку історію версій, щоб ви могли повернутися назад, якщо виникнуть нові помилки.
Чим швидше ви виявите невідповідність, тим більше впевненості ви будете мати у своїх числах.
Питання та відповіді щодо розрахунку складних відсотків
Одне питання, яке я чую постійно, це як впоратися з відсотковими ставками, які змінюються в середині інвестиції. Трюк полягає в тому, щоб розділити ваш часовий проміжок на сегменти та застосувати формулу нарахування до кожного з них.
Уявіть, що ви фіксуєте 5-річну інвестицію з доходом 4% протягом перших 2 років та 6% протягом наступних 3 років. Спочатку ви б розрахували:
A₁ = P × (1 + 0.04)²
Потім використовуйте A₁ як вашу нову основну суму:
A₂ = A₁ × (1 + 0.06)³
Помножте ці результати, і ви отримаєте вашу остаточну суму. Це звучить як додаткова робота, але як тільки ви побачите це в електронній таблиці, кожен елемент стає на місце.
Регулярні внески трохи відрізняються — вони поводяться як серія грошових потоків. Щоб впоратися з ними, ви будете спиратися на майбутню вартість ануїтету. Пам'ятайте про ці моменти:
- Використовуйте формулу майбутньої вартості ануїтету, коли ви робите регулярні внески
- Точно узгоджуйте вашу відсоткову ставку та частоту нарахування
- Визначте, чи внески відбуваються на початку чи в кінці кожного періоду
Для інвесторів, які прагнуть теоретично максимального доходу, безперервне нарахування вступає в гру з A = P e^(r t). Воно замінює звичайну дискретну формулу, коли ви припускаєте, що відсотки нараховуються нескінченну кількість разів.
Дискретне проти безперервного нарахування
Дискретне нарахування нараховує відсотки через регулярні проміжки — щомісяця, щоквартально або щорічно. Кожна подія нарахування трохи підвищує ваш баланс, збільшуючи загальні доходи, коли ви нараховуєте частіше.
Безперервне нарахування доводить цю ідею до межі, нараховуючи відсотки нескінченну кількість разів. На практиці це забезпечує найвищий можливий результат для заданої ставки та терміну.
Безперервне нарахування дає невелику додаткову перевагу, коли частота перевищує щоденні нарахування.
Знання того, який метод використовує ваш банк або калькулятор, заощадить вам головний біль при порівнянні пропозицій.
Завжди перевіряйте це налаштування у вашій електронній таблиці або фінансовому інструменті.
Обробка нульових та негативних ставок
Ставки на рівні або нижче нуля можуть здаватися нелогічними, але математика проста. При r = 0 ваш баланс ніколи не змінюється—A залишається рівним P. Негативні ставки зменшують ваш баланс з кожним періодом, ілюструючи, як витрати з'їдають ваш капітал.
- При –2% річній ставці ваш баланс зменшується на 2% щороку.
- Якщо ви перейдете на щомісячне нарахування, кожен період застосовує r/n = –0.02/12, тому втрати прискорюються з частішими інтервалами.
Остерігайтеся прихованих зборів, представлених як негативні ставки. Завжди підставляйте чисту ставку після зборів, щоб уникнути несподіванок.
Більшість онлайн-калькуляторів дозволяють вводити негативні числа—просто підтверджуйте, що інструмент показує A < P, коли r нижче нуля. Ця швидка перевірка здорового глузду забезпечує, щоб ваші прогнози залишалися на правильному шляху.
Готові спростити свої розрахунки? Спробуйте Калькулятор складних відсотків у ShiftShift Extensions. Моделюйте ставки, частоти та регулярні внески, не виходячи з вашого браузера.
Стаття створена за допомогою Outrank